有 n n 条直线，在正无穷处往下看，如果一条直线的某一部分没有被其他任何直线覆盖，则我们认为这条直线是可见的，输出所有可见直线的编号。

题解

我先描述一下算法。

首先对所有直线按照斜率从小到大，截距从大到小排序。然后把最小的两条斜率不想等的直线放到一个栈里，每次向栈中加入一条直线时检查即将加入的直线和栈顶直线的交点和栈顶直线和栈第二位直线的交点的位置关系，若新直线与栈顶直线的交点在栈顶直线和栈第二位直线的交点左边，则将栈顶元素弹出，若在右边，则将新直线入栈。最后栈中的直线就是答案。

下面形象的解释一下它的正确性。

首先，我们要维护的应该是一个下凸壳（就是说起来形象一点）。。

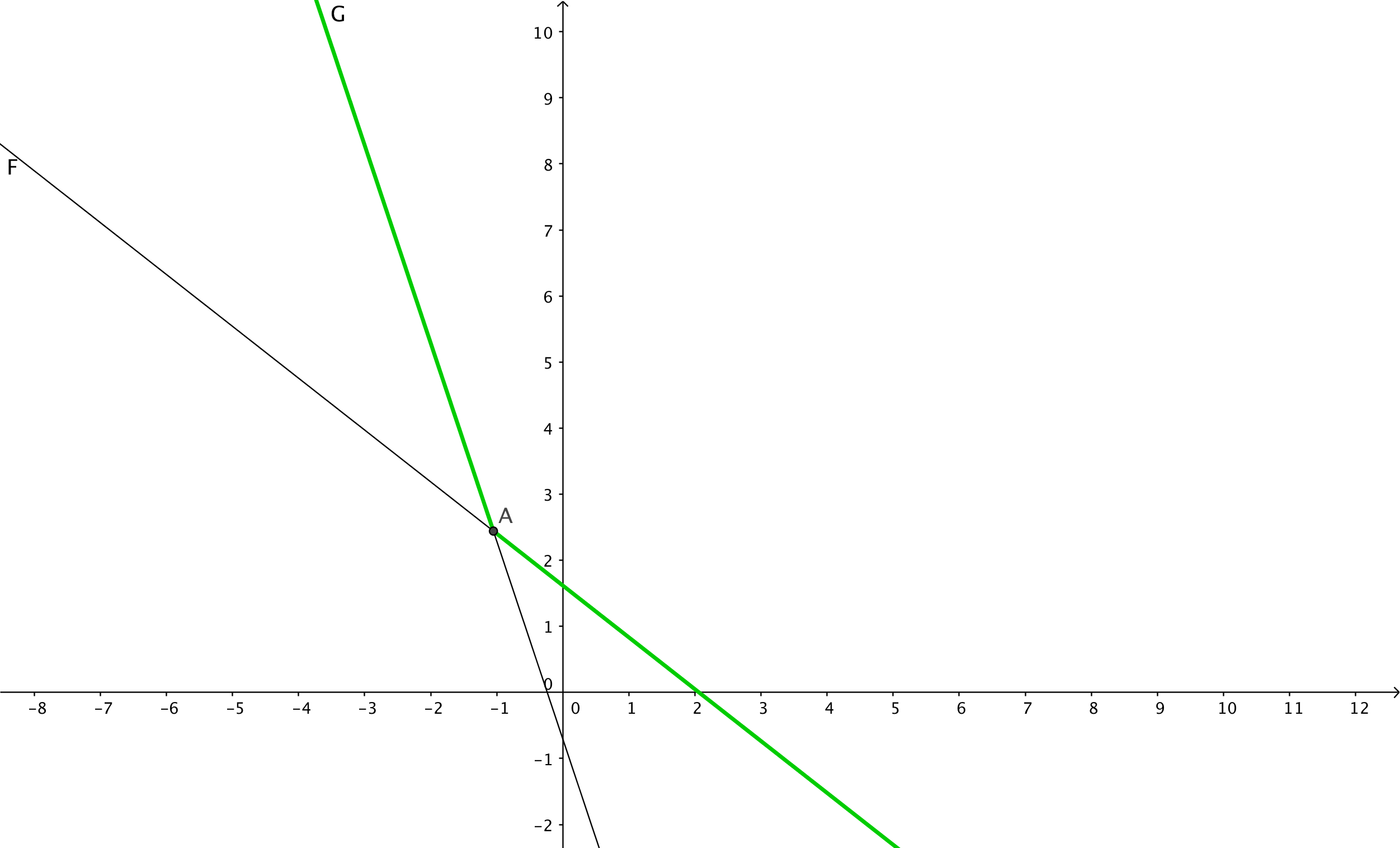
假设这是栈中的两条直线，则 F F 为栈顶直线，G G 为栈第二位直线。绿色部分就是目前合法的下凸壳。

Original

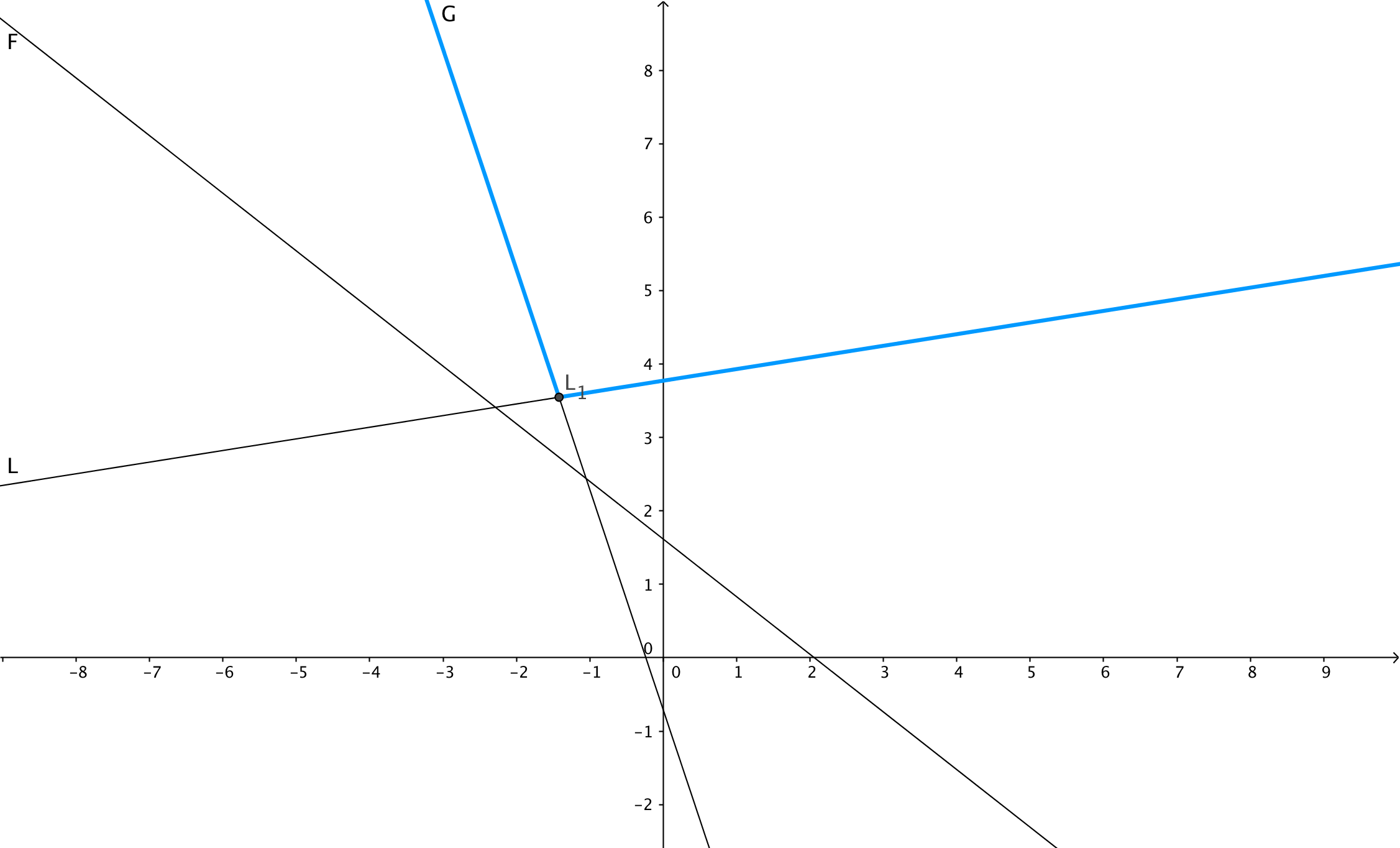
现在插入直线 L L ，交点在右侧，此时凸壳变成了蓝色部分，此时栈顶直线 F F 已经变为不可见的，就把它出栈。

Left

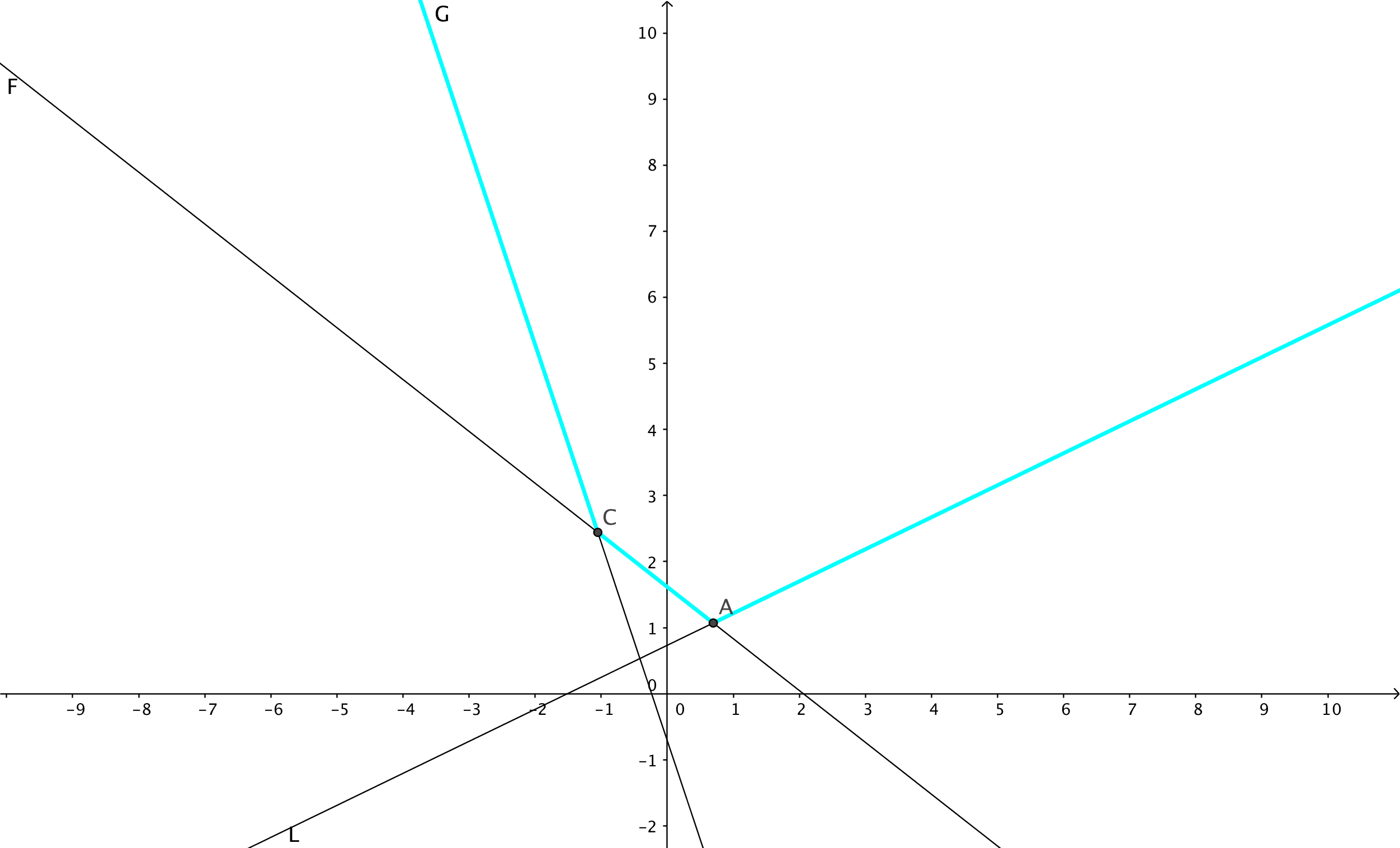
若直线 L L 和栈顶直线的交点在左侧，凸壳就变成下图状态，此时原栈顶直线仍然可见，则直接将直线 L L 入栈。

Right

其实用语言来描述就是，排序以后保证栈顶元素下面的元素一定可以覆盖住它的一半，而只有一条斜率更大的直线才能覆盖住它的另一半，所以只需要检查新加入的斜率更大的直线是否能够完全覆盖未被覆盖的部分就可以了。

代码

#include <cstdio>
#include <cstring>
#include <climits>
#include <cmath>
#include <cfloat>
#include <algorithm>
const int MAX_N = 50000;
const double EPS = 1e-8;
struct Line {
    double k, b;
    int id;
    bool operator<(const Line &other) const {
        if (fabs(k - other.k) < EPS) return b > other.b;
        return k < other.k;
    }
} l[MAX_N + 1];
int n;
int s[MAX_N + 1], top = 1;
bool ans[MAX_N + 1];
inline double calc(Line a, Line b) {
    return (b.b - a.b) / (a.k - b.k);
}
inline void solve() {
    memset(ans, 0, sizeof(ans));
    std::sort(l + 1, l + n + 1);
    s[top] = 1;
    for (int i = 2; i <= n; i++) {
        if (fabs(l[i].k - l[i - 1].k) < EPS) continue;
        while (top > 1 && calc(l[i], l[s[top]]) <= calc(l[s[top]], l[s[top - 1]])) top--;
        s[++top] = i;
    }
    for (int i = 1; i <= top; i++) {
        ans[l[s[i]].id] = true;
    }
    for (int i = 1; i <= n; i++) {
        if (ans[i]) printf("%d ", i);
    }
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%lf %lf", &l[i].k, &l[i].b);
        l[i].id = i;
    }
    solve();
    return 0;
}